画像 三角形 定理 324191-三角形定理

拿破侖定理 Wikiwand
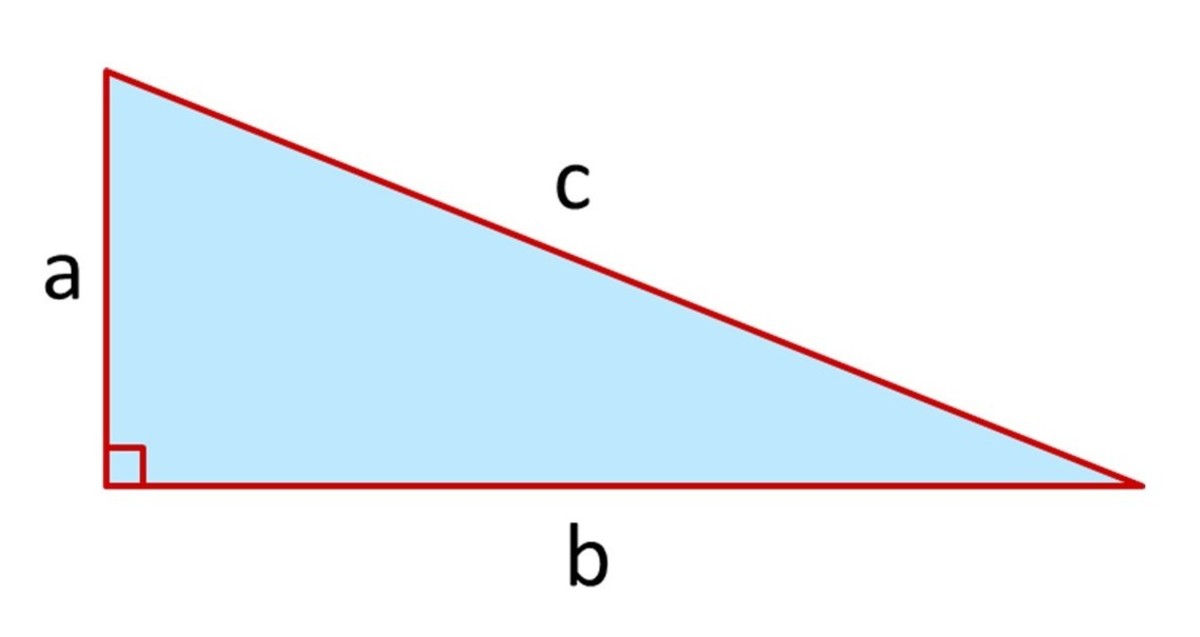
次のような直角三角形の3辺の長さについては, a 2 b 2 =c 2 が成り立ちます.(これを 三平方の定理 といいます.)余弦定理可以理解为是勾股定理在一般三角形中的扩展。勾股定理解决直角三角形的边关系问题,余弦定理则解决所有三角形的边角关系问题。所以余弦定理公式也是勾股定理的基础上,增加了角度要素而成。 余弦定理有什么用? 正、余弦定理都是解三角形的重要依据。 余弦定理适用的条件是什么?
三角形定理
三角形定理-三角関数の加法定理,倍角公式,3倍角公式,半角公式 三角関数の和や積には多くの公式がありますが,「加法定理は覚える,他は作る」というのが,作者おすすめの考え方です。・・・ただし,そういう公式があるということと,およその形は記憶にとどめます。 これだけは覚えよう (2)(4)を三平方の定理が使えるのは直角三角形である。 定理を利用する場合は図から直角三角形を探すか、補助線を書いて直角三角形を作る。 座標上での2点間の距離 いままで、座標上で斜めの長さは出せなかったが、三平方の定理を使えば出せるようになる。 a b 例図の線分abの長さを求める。 x
梯形蝴蝶定理 燕尾定理与蝴蝶三角形 尚书坊
定理:三角形 a b c abc a bc の内接円と辺 b c bc bc の接点を d d d とおく。 d d d から辺 b c bc bc と垂直な直線と内接円の交点を e e e とおく。さらに a e ae a e と b c bc bc の交点を f f f とおくとき, b d = c f bd=cf b d = cf → 内接円に関する数オリ頻出の図形 正方形の頂点と最短距離 問題 正方形の4 断面二次モーメントの公式を求めるために必要な知識は2つだけです 断面二次モーメントの計算式 平行軸の定理の使い方 三角形の断面二次モーメントを求める手順は全部で4ステップです ①計算が容易になるz軸を決める ②微小面積dAを求める ③計算が容易なz軸に関して断面二次モーメントを求める ④平行軸の定理を用いて解を出す 三角形の断面二次 \(bcd\) は直角三角形なので、その3辺について三平方の定理 \(bc^2=cd^2db^2\) が成り立ちます。 ここに \(BC,CD,DB\) の値を代入すると・・・ 余弦定理が成り立ちます。
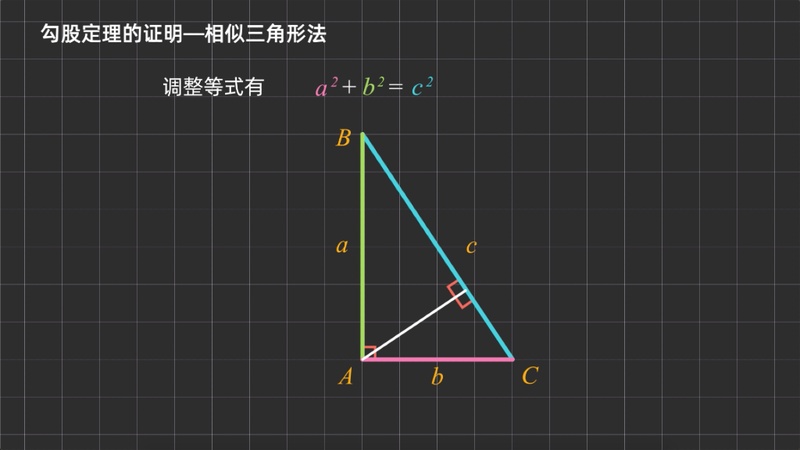
ピタゴラスの定理とは、古代ギリシアの数学者で哲学者のピタゴラスが立ち上げた団体が発見した数学の定理のこと。直角三角形をなす3辺のうち、2辺の長さを知ることができれば、残り1辺の長さを知ることができるというものです。 公式:a² b² = c²正弦定理を三角形の面積と関連付けます。 ※ 図は Markdown に SVG を直接記述しています。詳細はこちらをご参照ください。 正弦定理 図 1 A B C 2R a b c 教科書でよく見る形の正弦定理は、円の直径との関係を含んだ形で記述されます。 三平方の定理 別名:ピタゴラスの定理 三角形において、成り立つ公式です。 \(\angle C = 90^{\circ} \Longleftrightarrow a^2b^2 = c^2\)
三角形定理のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 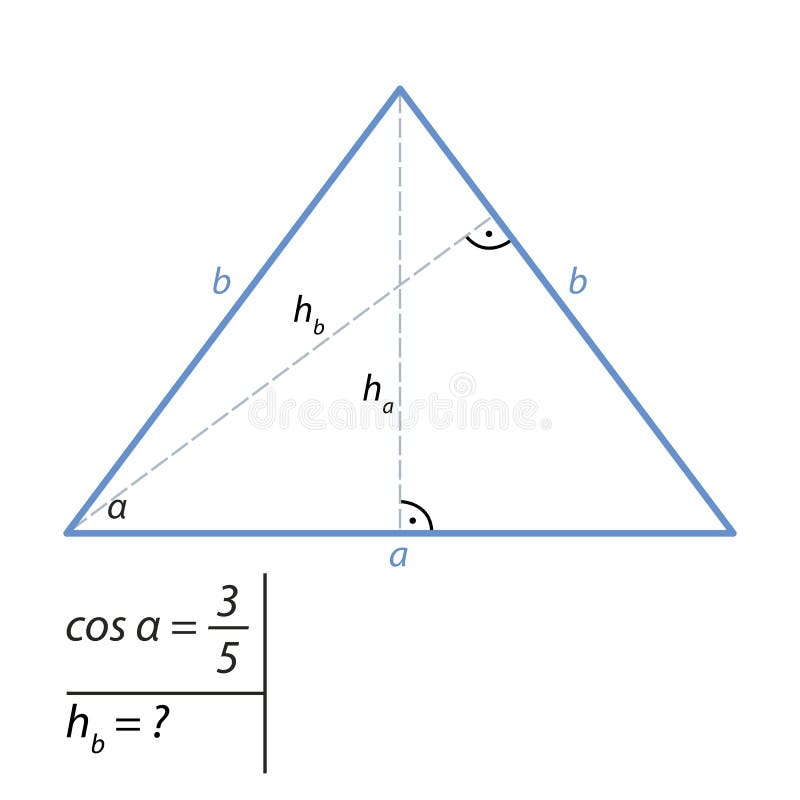 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 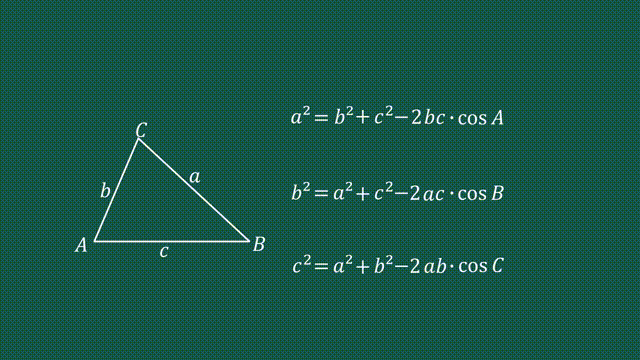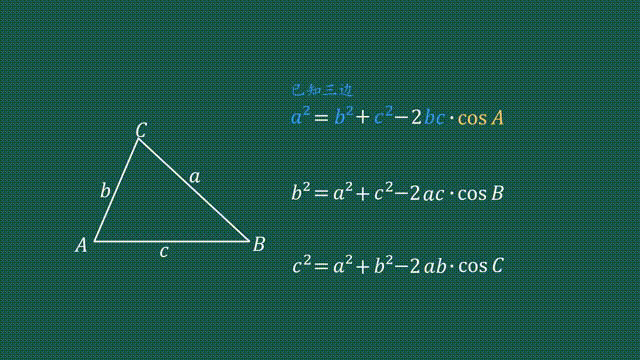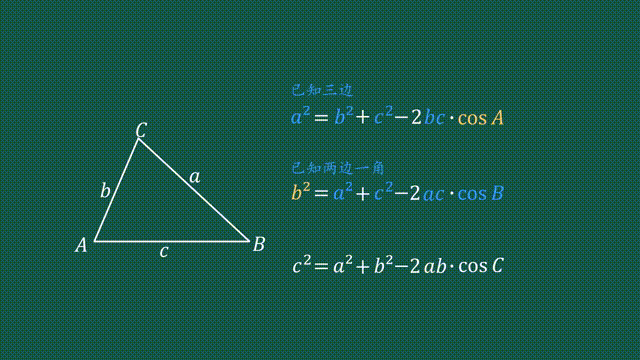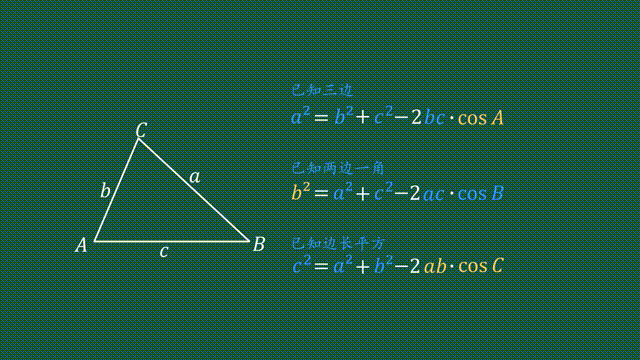 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 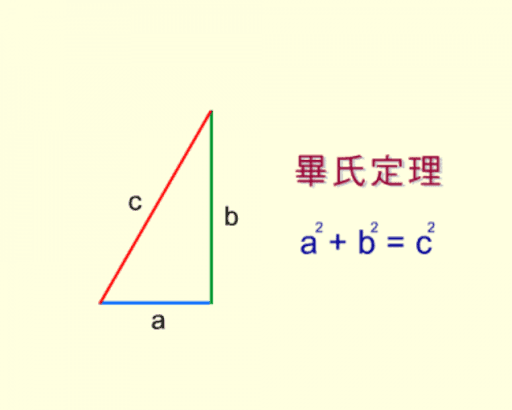 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |  发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 | 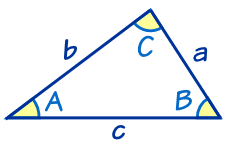 发现一个正三角形的高度的问题由勾股定理的库存例证 插画包括有 |
正弦定理から,三角形の辺の長さを求める計算について ABCにおいてa = 3 ,A = 60°,B = 45°のときbを求めよ。 という問題がありますが, これを定理にあてはめていって, b = 3 / sin60°× sin45° まではつくれるんですが,そこから (3 ÷ √3/2 ) × 1/√2= 6/√6=√6 というのになるのが,意味がわかりま 三角形全等的判定定理是什么 1621 文/宋则贤 经过翻转、平移后,能够完全重合的两个三角形叫做全等三角形。而该两个三角形的三条边及三个角都对应相等。全等三角形指两个全等的三角形,它们的三条边及三个角都对应相等。 三角形全等的判定定理 (1)三边对应相等的三角形
Incoming Term: 三角形定理, 三角形定理大全, 三角形定理公式,
コメント
コメントを投稿