√99以上 3角関係 104435

141 軌道角運動量演算子と交換関係 3 (143) の導出 L2 = LL とL の成分との交換関係は，(149) を用いて L2,Li= j LjL j,L i j L j L j,L iL j,L iL j = jk i jikL jL k jk i jikL kL j と書ける。ここで，最右辺の第2項で，まず，和をとる2つの添字j とk を交換し，つい で jik の反対称性 kij = − jik を用いる：させると3つのデータはほとんど一致する．σbが小さ な領域では軸応力と回転角の関係が顕著な非線形性を 示していることから，回転角を基準として締め付ける 前に，スナッグトルクTfsを与えること概要 三角関数（度） サイン、コサイン、タンジェントなどの三角関数を度単位で計算します。 三角関数（グラフ） sin、cos、tanの関数表を計算し、sinとcosのグラフを表示します。 逆三角関数（度） アークサイン、アークコサイン、アークタンジェントなどの逆三角関数を度単位で計算します。 角度と底辺から斜辺と高さを計算 直角三角形の底辺と傾斜角から

三角関係イラスト 無料イラストなら イラストac

3角関係

3角関係-余弦定理を変形すれば、 b , c , a が分かっているときに A を求めるという使い方もできます： a 2 =b 2 c 2 −2bc cos A この式をよく見ると、 「右辺は辺の長さだけ」 でできており、 左辺は角度だけ でできています。 したがって、この式を利用すると 「3辺の 4角関係！？5角関係！？ 3話 12 作品ページ さぁちゃんモテすぎやろw

三角関係に揺れる少女マンガ特集 キャンペーン 特集 漫画 無料試し読みなら 電子書籍ストア ブックライブ

り ️ぬ 性格 恥ずかしがり屋 好きな人 いない 特徴 泣き虫 ジ🧡ル 性格 エロい3 三角関数の相互関係 ( 1 ) θが第3象限の角で，sinθ＝－ のとき，cosθ，tanθの値を求めなさい。 (2 ) θが第4象限の角で，tanθ＝－2のとき，cosθすくい角について説明できる。 逃げ角について説明できる。 切れ刃角について説明できる。 切削抵抗 切削抵抗の3分力を説明できる。 背分力の影響を説明できる。 構成刃先 構成刃先について説明できる。 構成刃先を防ぐ手法を説明できる。 切削油剤

 3つのパターンから分かる円周角と中心角の関係性 Tooda Yuuto 18年8月2日 / 18年12月21日 「同じ弧 A B に対する円周角 ∠ A P B, ∠ A P ′ B は等しく、同じ弧に対する中心角 ∠ A O B の半分である」という定理を、 円周角の定理 と言います。 円周角の定理の証明には ① 「円周角 ∠ A P B の内側」に円の中心 O がある ② 「円周角 ∠ A P B の線分上」に円の中心 O がある切削抵抗は、切削する際に被削材がバイトを押し戻そうとする力のことです。 力のかかる方向によって、主分力・送り分力・背分力の3つに分けられ、これらの合力を切削抵抗といいます。 等の条件によって変化します。 これらの項目と、切削抵抗の関係 光の屈折の法則3分でわかる！入射角と屈折角の関係の覚え方 光の屈折の法則で、入射角と屈折角の関係がわからない！ こんにちは！この記事を書いているKenだよ。のど飴、100個ぐらい欲しいね。 中学1年生の理科では、 光の屈折の法則 を勉強して

 答えは否で、例えば を3辺にもつ三角形は存在しないこと分かるでしょう。 三角形が存在する条件、つまり三角形の成立条件を一般的に数式で表すには「三角形の1辺の長さは他の2辺の和より小さい」ことを利用します。 「」内を数式で表すと ・・・① かつ ・・・② かつ ・・・③ です。②は , ③は となるので、②③をまとめると であり、①と合わせると と交換関係は座標軸の回転から求められ，軌道角運動量演算子と同じ交換関係であるが，角運 動量の値として整数だけでなく半奇数も許される。J =(1/2)¯h はフェルミ粒子がもつ内部 自由度としてのスピン角運動量に対応する。 101 極座標 1011 デカルト座標とせん断角理論 （せん断角を求める理論。せん断角から切削抵抗やせん断歪も決定できる。） 直線すべり線場モデル(Lee & Shaffer, 1951) 剛塑性境界AO、主応力面AB、工具すくい面BOで囲まれる三角 形領域を塑性域と仮定。最大せん断応力方向（すべり線）は互い

Hugedomains Com Incoming Call Screenshot

三角関係の写真素材

「脱原発・脱市場 不屈の日本再生！ 」6 〜原発推進の3角関係〜 「 一体、この国の原発はどうなってんの？ 」 「 っていうか、なんで日本の狭い国土に57基も原発あるの？ 多くない ？ 」 という 素朴な疑問 を持つ人が増えています。の3角関係！？のお話・・・ 布川俊樹、実は彼と僕はほぼ毎日とまではいきませんが、 1週間に3日くらいは顔を会わせてます。 っというのも、某大学でどちらもギター講師という身分で お仕事をやらさせて頂いておりまして（ありがたや～）3倍角の公式とは、角 3α の三角関数（左辺）を、角 α の三角関数に変換する（右辺）公式です。 \begin{align*} \sin3\alpha &= 3\sin\alpha 4\sin^3\alpha \\5pt \cos3\alpha &= 4\cos^3\alpha 3\cos\alpha \\5pt \end{align*}

三角関係の男性2人と女性 の写真素材 イラスト素材 アマナイメージズ

二等辺三角関係 Pixiv年鑑 B

 角の大きさと辺の長さの関係 基本よく出る0度から180度までの三角比の値#三角比のとる値の特徴で見た通り、90度以下の範囲では、角の大小関係と $\sin$ の大小関係は一致します。これに正弦定理を組み合わせれば、辺の大小関係とも関連付けることができます。P = T × θ t W又は J/s 動力=トルク×角速度 P = T × ω W 又は J/s 回転速度 N rpmの場合の公式 動 力 = ト ル ク × 2π × 回 転 速 度 60 P = T ･ 2πN 60 ≒ TN 9549 W又は J/s 工学単位を使った動力の計算式 トルク T kgf･m 動 力 = 2πTN 60 × 102 kW ≒ TN 975 kW三角比 sin A , cos A , tan A のうち1つ分かれば、残りはこれらの公式を使って「芋づる式に」求まります。 例えば、 sin A が分かれば(1)を使って cos A が求まり、さらに(2)を使って tan A が求まります。 しかし、例えば tan A = のように、三角比のうちで tan A だけが与えられて残りの sin A , cos A を求め

三角関係 さんかくかんけい 意味類語辞典

絶対ハッピーエンドになる三角関係

 三角関数の復習 基本三角関数の定義 では、一般角に対して三角関数を定義しました。 O(0,0) O ( 0, 0) を中心に A(1,0) A ( 1, 0) を反時計回りに θ θ だけ回転したときに、 P(x,y) P ( x, y) に移るとすると、 sinθ = y,cosθ = x,tan = y x sin ⁡ θ = y, cos ⁡ θ = x, tan = y x となるのでした（ x = 0 x = 0 のとき、 tan tan は定義しない）。 本来は、半径が r r の円を使って定義すべき 問題編三角形の辺と角の大小関係と成立条件 問1 次の ABCについて、角や辺の大小関係を答えましょう。 (1) \(\angle A=100^\circ、b=4、c=2\)のとき、3つの角の大小関係 →答え1_2 周期・周波数・角速度 先ほどは角θの値によってsin波 f(θ)＝a sinθ と cos波 f(θ)＝a cosθ が変化していく様子を見ました。今度は角θも時間とともに変化させてみましょう。

ポエム 三角関係の画像303点 完全無料画像検索のプリ画像 Bygmo

三角関係の写真素材

 三角比の基本でもあり重要公式である「三角比の相互関係」。 3つの公式と、その使い分けについて説明していく。 三角関数の基本的な知識や注意点について さきほども紹介したが、sinやcos、tanは必ず基準となる角の大きさとセットで使わなくてはならない。昭和学土会誌第76巻第6号〔 頁16 〕 原著 立位における腰椎，骨盤，下肢の矢状面上の アライメントパラメータ一間の関係x線写真計測値を用いた検討一 "昭和大学大学院保健医療学研究科 2）社会福祉法人あそか会あそか病院リハビリテーション科 3）昭和大学医学部整形外科学講座角速度との関係 オイラー角の微分 と角速度 の関係式を導くには、 （式( )） の右辺に式( )を代入して、両辺を比較すればよく、以下のようになる： なお、 の時、この行列の第1列と第3列が平行になって、逆行列を持たなくなってしまう。

ツイステ 三角関係 監督生 ガッツリ出てます なんでも許せる監督生さんだけ キャベ子の漫画 漫画 作品 絵

女の子三人の三角関係を描いた百合読み切り ゆずれない が少年エースに掲載 百合ナビ

Q1 前回学んだ三角形の相互関係の式の他に、もう一つの相互関係の式として正しいものを1つ選びなさい。 Q2 θ が第4象限の角で、cosθ＝2√2／3の上のような円があったとします。 大きさは何でもいいです。 この円の上に点を3つ乗せていくと、 このようになります。 点はそれぞれ、点A,点B,点Cとしておきます。 次に、乗せた3つの点の2つの線分でつないでいきます。 こうすると、線分と線分に挟まれた点Bのところに、角が出来ていることが分かります。 この角を、線分を構成するA,B,Cを用いて∠ABCと表せことにより，上肢挙上角と矢状面上の脊柱彎曲角との 関係について検討した。 II 対象と方法 1 対象 対象は，健常成人男性12名とした。いずれも上肢や 体幹に疼痛や不安感などの既往はなかった。年齢は平 均236±55歳，身長は平均1697±38 cm，体重は平均

三角関係の写真素材

ネタバレ感想 合格のための やさしい三角関係入門 第6話 陽光の下で 月刊コミック 電撃大王年8月号 社畜の漫画アニメネタバレ感想ブログ

 3角関係の地獄は爆サイcom東海版の愛知新型コロナ・感染症掲示板で今人気の話題です。 3角関係の地獄の情報交換はこちらで。利用はもちろん無料なので今すぐチェックをして書き込みをしよう！ 投稿：998件 最新の投稿日時： 16223 角運動量の合成 軌道角運動量演算子の交換関係を基礎にして、角運動量の概念を一般化できる。一粒子 のスピン軌道結合効果、多粒子系の全角運動量とそれに関連した物理的性質を定量的に議 論するには一般化角運動量を合成する必要がある。

三人が恋愛関係に陥った状態を三角関係といいます 1 ボーイズファン 矢上真野 ボーイズラブマンガ Kindleストア Amazon

キャラクターの作り方 三角関係 アニメ ハイスコアガール におけるエニアグラム がんべあの ぶれない キャラクター ストーリーの作り方

合格のための やさしい三角関係入門 1 電撃コミックスnext 缶乃 本 通販 Amazon

最高にホッコリする高校生の三角関係 男は女に敵わないとわかる10のエピソード 笑うメディア クレイジー

毎日がバーゲンセール 新品未開封 Cd 素敵関係三角関係 Kicj 816 Feat 三浦拓也

本命はどっち 複雑な三角関係が一目で分かる写真とは じゃみログ 雑学 トリビア 裏話

どんな 三角関係 タイプ診断 Mirrorz ミラーズ 無料の心理テスト 診断 占い

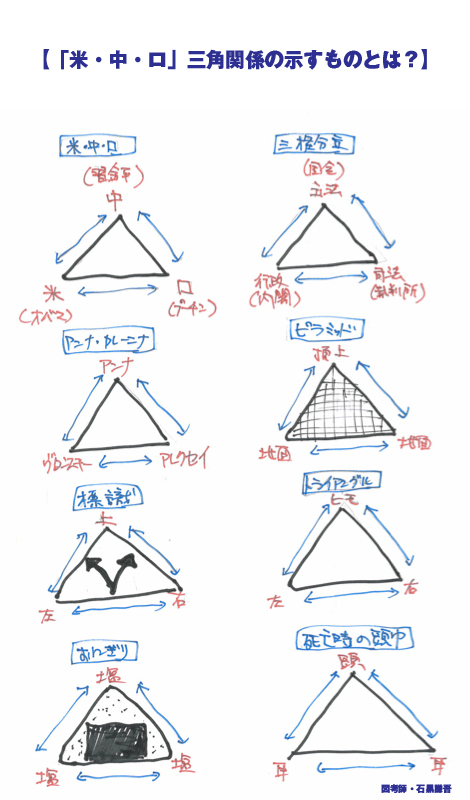
最も選択された 三角関係とは 三角関係とは Sabrinasharrowjp

絶対ハッピーエンドになる三角関係 1 ヤングジャンプコミックス 梅田 ぴよ 本 通販 Amazon

三角関係になるきっかけとは 三角関係に巻き込む女性の特徴 対処法を解説 Smartlog

こんな三角関係だなんて聞いてません Bl小説 小説投稿サイトのアルファポリス

恋愛の三角関係を解決するには 対処法を知れば悩みもスッキリ ラブサーチマガジン

合格のための やさしい三角関係入門 無料漫画詳細 無料コミック Comicwalker

3角関係のマンガのtwitterイラスト検索結果

止めた方がいいでしょう 三角関係の夢占い 夢占いの館

禁断の青春ラブストーリー映画 恋と嘘 で森川葵 北村匠海 佐藤寛太が三角関係に 17 04 03 邦楽ニュース 音楽情報サイトrockinon Com ロッキング オン ドットコム

乙女ゲー初心者にオススメな 片恋いコントラスト 第3巻を紹介 教師と転校生 どちらを選ぶかはあなた次第

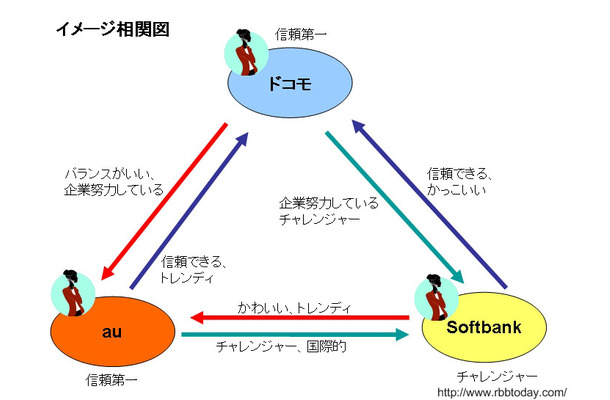
ユーザが抱く携帯キャリアのイメージ その 三角関係 とは ネットエイジア調べ Rbb Today

ふたりなのに三角関係 松村北斗 Sixtones 森七菜w主演 映画 ライアー ライアー 本予告映像公開 音楽webメディア M On Music エムオンミュージック

Blラバーの書店員がおすすめする 三角関係なbl 2選 好書好日

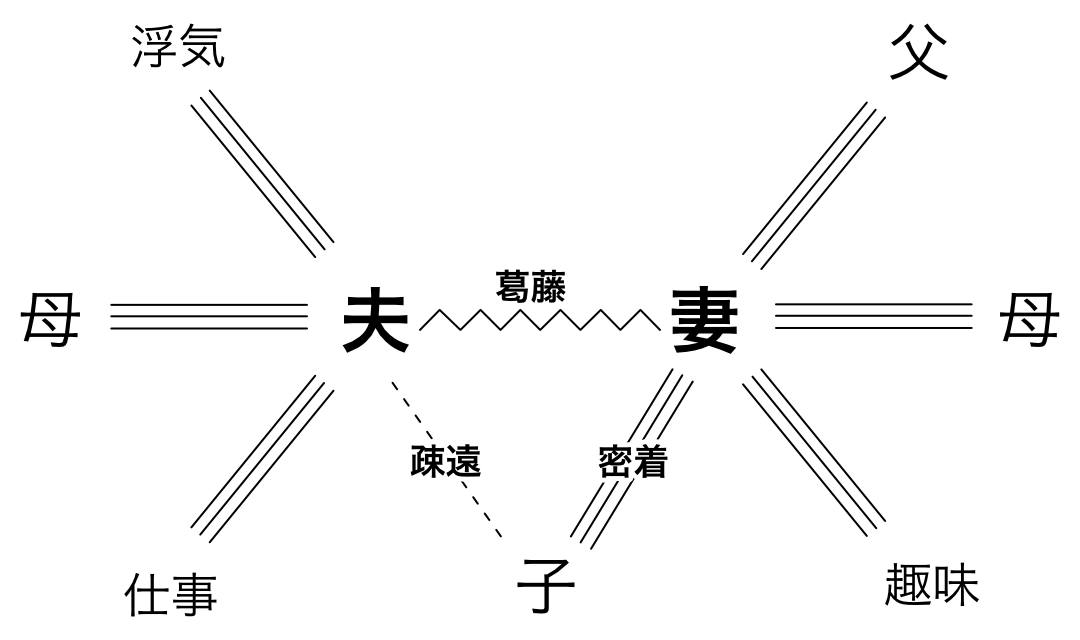
三角関係は夫婦 家庭の危機のサイン 大阪 北摂 吹田市 のカウンセリングルーム

凪のお暇 おっさんずラブ 三角関係が面白いドラマランキング 16 19年放送 9 10位 ランキングー

三角関係を描いた恋愛漫画まとめ 無料試し読みもできる漫画 電子書籍ストア めちゃコミック

三角関係の恋愛ドラマの動画視聴なら 初月無料 動画配信サービスのビデオマーケット

三角関係を描いた恋愛漫画まとめ 無料試し読みもできる漫画 電子書籍ストア めちゃコミック

三角関係イラスト 無料イラストなら イラストac

三角関係を描いた恋愛漫画まとめ 無料試し読みもできる漫画 電子書籍ストア めちゃコミック

テーマは三角関係 オトメイトｘフロンティアワークスのゲームプロジェクト Triangle Project 始動 にじめん

山田菜々主演 マスタード チョコレート 4月29日公開 三角関係を匂わすキービジュアルも 映画ニュース 映画 Com

三角関係を描いた恋愛漫画まとめ 無料試し読みもできる漫画 電子書籍ストア めちゃコミック

合格のための やさしい三角関係入門 月刊コミック電撃大王公式サイト

三角関係のイラスト素材

恋と友情どちらが大事 三角関係の悩みを解消 ラブコスメ

三角関係マンガを探す 恋エピ

特集 純愛三角関係 私が好きになった人 私を好きになってくれた人二人の 好き に挟まれて どうしたらいいかわからない まんが王国

三角関係を描いた恋愛漫画まとめ 無料試し読みもできる漫画 電子書籍ストア めちゃコミック

３人グループによくある光景 凄く面倒な三角関係 話題の画像プラス

三角関係 さんかくかんけい とは ピクシブ百科事典

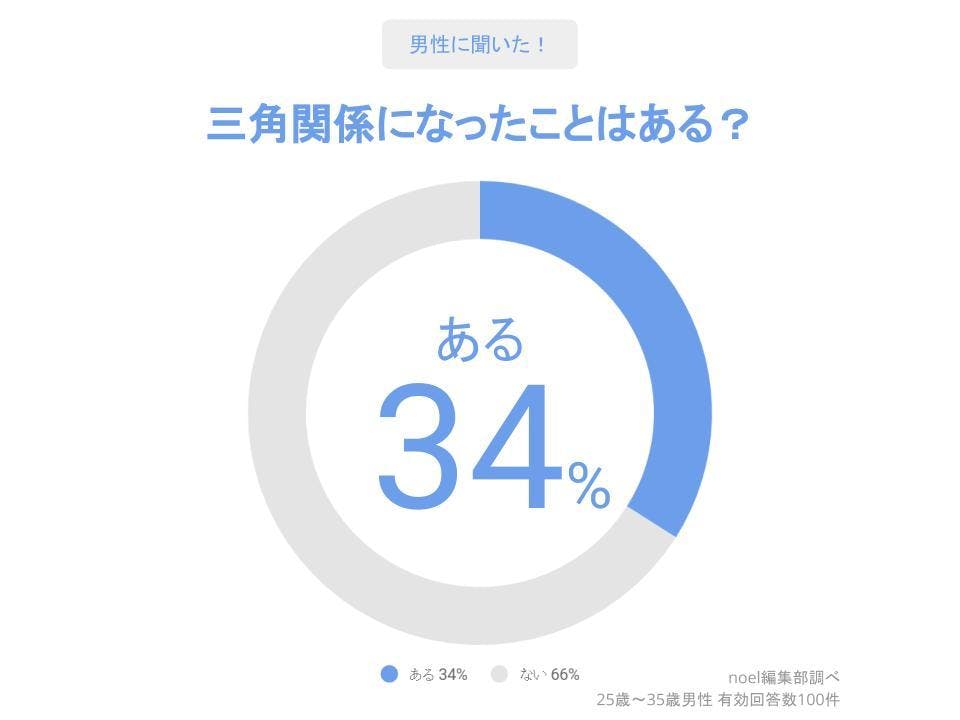
三角関係にハマりやすい女性の特徴 三角関係を描く映画 ドラマ5選 浮気 Noel ノエル 取り入れたくなる素敵が見つかる 女性のためのwebマガジン

三角関係の構造 笑 Georgie717のブログ

ときめきメモリアルgs３ 三角関係 先輩編 キノミキノママ

三角関係に揺れる少女マンガ特集 キャンペーン 特集 漫画 無料試し読みなら 電子書籍ストア ブックライブ

三角関係のイラスト素材

伏虎 五悠と伏虎で三角関係まんが 3 1 あずま紅の漫画

三角関係 強引な女子から守ってくれた彼 貴色さんのマンガ

好きになった人は元カレの弟 Lineマンガで第1位を獲得した胸キュン三角関係ラブストーリー ブラザー トラップ 第 巻 12月15日 土 発売 株式会社kadokawaのプレスリリース

イケない三角関係 らぶトライアングル らぶドロップス 鍬津ころ 長谷川ゆう ライトノベル Kindleストア Amazon

辛い三角関係に円満な終止符を 男女別の特徴と対処法 ベラスパ Belluspa

三角関係を描いた恋愛漫画まとめ 無料試し読みもできる漫画 電子書籍ストア めちゃコミック

三角関係の意味 用法を知る Astamuse

三角関係の面白ネタ 写真 画像 の人気まとめ タグ ボケて Bokete

三角関係の パターン別対処法 を男女心理のプロが解説 マイナビウーマン

マンガ家の仕事場が舞台の三角関係ラブコメ 絶対ハッピーエンドになる三角関係 コミックナタリー

四角関係 の読み方に関する一考察 あとーすログ

三角関係 をテーマにしたゲームプロジェクト Triangle Project が始動 アニメイトタイムズ

三角関係になってしまったら 陥りやすい人の特徴と対策を知ろう Mine マイン

三角関係に巻き込まれました 下の図を見ていただけると分かる通り私は Yahoo 知恵袋

三角関係 素材の画像76点 完全無料画像検索のプリ画像 Bygmo

ドキドキの三角関係を描いたおすすめ韓国ドラマ10選 Lovekach ラブカチャンネル

三角関係イラスト 無料イラストなら イラストac

三角関係に巻き込んでくる女性の特徴7選 三角関係に陥らないための対策を紹介 恋学 Koi Gaku

広告コミュニケーション 三つのメディアと三角関係 概念図 マーケティングのアイデア デジタルマーケティング

ハート 恋愛 三角関係 三人 ライバルのイラスト素材

三角関係に揺れる少女マンガ特集 キャンペーン 特集 漫画 無料試し読みなら 電子書籍ストア ブックライブ

三角関係 プロローグ 完全無料画像検索のプリ画像 Bygmo

三角関係の女性2人と男性 の写真素材 イラスト素材 アマナイメージズ

あのキスの缶乃先生が描く三角関係ラブストーリー 合格のための やさしい三角関係入門 が電撃大王 Webでスタート 百合ナビ

両手にイケメンな三角関係特集 小学館eコミックストア 無料試し読み多数 マンガ読むならeコミ

絶対ハッピーエンドになる三角関係 第14話 Free Raw 最新マンガ 無料漫画

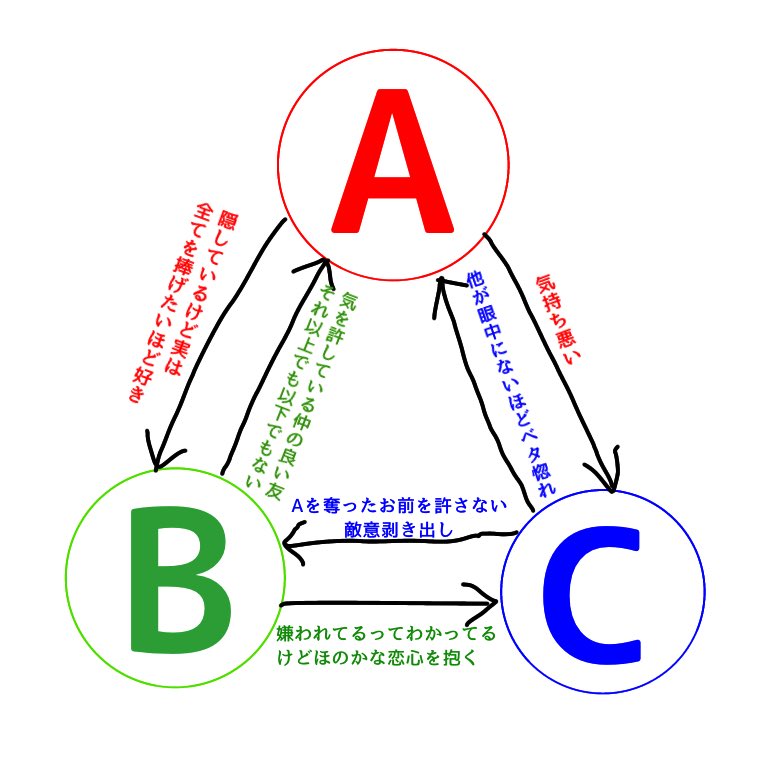
カサ子は原稿やれ على تويتر こういう三角関係があったとして じゃあこのa Cの中で誰か一人死ぬってなったら 誰をころすかでその人の性癖がわかってしまうと思うんだなあ みつを

彼と親友の三角関係 私が選んだ道 恋エピ 漫画 マンガ動画 Youtube

17歳キャロラインの三角関係 映画情報 レビュー 評価 あらすじ Filmarks映画

缶乃 三角関係入門 3 26 本日発売の電撃大王に 合格のための やさしい三角関係入門 3話が掲載されています 2話で凛に相談を受けたあとのあきらの話です なにかとこじれてきました よろしくお願いします

三角関係 あなたには経験ありますか 映画 ドラマで描かれたせつな系三角関係 Middle Edge ミドルエッジ

三角関係の力学 龍の吐息

三角関係に揺れる少女マンガ特集 キャンペーン 特集 漫画 無料試し読みなら 電子書籍ストア ブックライブ

ネタバレ感想 合格のための やさしい三角関係入門 第7話 Superluminal 月刊コミック 電撃大王年10月号 社畜の漫画アニメネタバレ感想ブログ

三角関係 マイナビウーマン

三角関係の女性2人と男性 の写真素材 イラスト素材 アマナイメージズ

三角関係のイラスト素材

三角関係のイラスト フリーイラスト素材 ガガフリー

三角関係の女性2人と男性 三角 関係 イラスト

気をつけろ 三角関係 に巻き込んでくる女子の特徴10パターン オモコロ

Blに関する質問 A B や A B C などの関係性を表す表記は Wikipediaより 人力検索はてな

三角関係 イラストの画像21点 完全無料画像検索のプリ画像 Bygmo

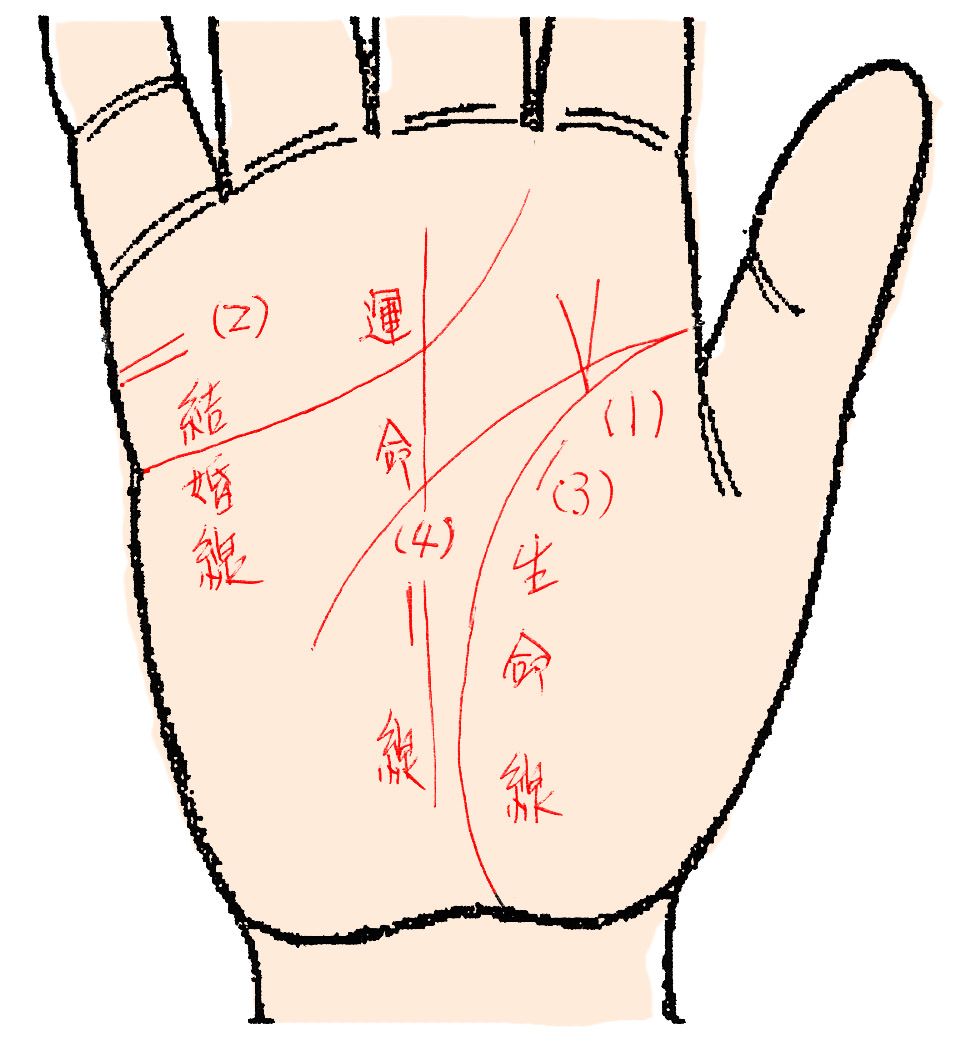
手相の話題59 三角関係を招きやすい 三角関係の相 達人に訊け 中日新聞web

三角関係の複雑な恋愛を占いで解いていく

男 女 男の幼馴染3人 いびつな三角関係描く サヨナラさんかく 1巻 コミックナタリー